The Search for the Elusive Theory of Everything

AN
10/23/2010

The elusive Theory of Everything (TOE) that combines quantum mechanics and general relativity has yet been successfully elucidated despite attempts by many theoretical physicists over the last 40 years. Since the two domains (the very small and the very large) are inherently of different nature, attempts to combine the two into a unified theory may be a futile attempt in theoretical physics. Instead, the two may be seen as two complementary theories that model processes in subatomic domain and macroscopic domain. Through decoherence, quantum entities change their probabilistic properties into deterministic properties in the macroscopic world. In this article, it is proposed that decoherence is not limited to the act of measurement by any conscious observer. Subatomic processes affect macroscopic processes, and vice versa, providing a dynamic interaction between the two domains.

1. Introduction

Quantum mechanics and general relativity are two of the most successful theories in physics, the former in explaining the three subatomic forces and the latter in explaining gravitational force on the cosmic scale of stars and galaxies [1]. Most theoretical physicists believe that it is not reasonable to have two theories covering two different phenomena in the same universe, as if the subatomic world and the cosmic world have nothing to do with each other [7]. Many have worked hard to obtain a TOE to combine quantum mechanics and general relativity. Several approaches have been pursued over the last 40 years. They include quantum loop theory, spin network, periodic lattice space-time, and string theory [7], to name a few. To date the exact equations for these theories are unclear, and important physical concepts remain to be discovered. Since the two domains of quantum mechanics and general relativity (the very small and the very large) are inherently of different nature, it is very likely that attempts to combine the two into a unified TOE may be a futile attempt in theoretical physics.

2. General relativity-the field equation

In general relativity, the position of a space-time point is uniquely defined by a set of four real numbers, three for space and one for time, specified as coordinates in an established coordinate system. According to general relativity, space-time is dynamical. It affects, and in turn is affected by, the particles that constitute space-time itself. Let us examine the components of the field equation of general relativity [2]:

G_{μν +} Λ g_μν = 8 π G T_μν (Eq. 1)

Where G_μν: curvature tensor

Λ: cosmological constant

g_μν : space-time metric tensor

T_μν: stress-energy tensor

G_μν is a function of g_μν and its first and second derivatives, in a precise mathematical technique by Newton and Leibniz. Coordinates in space-time represent position and time. Generality assumes that we know both the coordinates and momentum precisely at once. Subsequently, causality is established with precise momentum and coordinates of measured objects.

General relativity extends Newtonian mechanics with a set of field equations which relate the curvature of space-time with the mass, energy, and momentum within it. It is a classic theory that refines Newtonian mechanics to take into account very large objects and very large distances at cosmic scales.. It is mostly thanks to Isaac Newton that we can understand and predict how everyday objects move and interact under the influence of gravitational force [8]. Newtonian determinism has been the foundation on which scientific experiments were designed and natural processes were modeled. Newtonian mechanics was used by NASA to plot the trajectories of rockets to the moon and back. So why can't we apply the same types of equations to precisely determine the trajectories of subatomic particles, such as an electron? It turns out that the classic equations that govern the behavior of everyday life, from a grain of dust to soccer balls and planets, are not applicable in the subatomic domain of the quantum world.

3. Quantum mechanics-the uncertainty principle and the wave equation

Quantum mechanics dictates uncertainty in position and momentum of the particles in space-time with consequent subjection of geometry to quantum fluctuation. According to Heisenberg's uncertainly principle, the uncertainty in momentum and position of a particle (for example, an electron) is expressed as [3]:

∆p. ∆q > h/(2 π) (Eq. 2)

Where ∆p : uncertainty in momentum p

∆q : uncertainty in position q

h : Planck's constant

This equation shows that the more accurately we know about the particle position, the less certain we know about its momentum, and vice versa. The measurements of momentum and position are also rooted in classical physics even though it is known that classical physics does not apply in subatomic processes. In addition, the observer has to interfere with the subatomic process in order to measure them. Quantum theory indicates that point particles behave in some respects like waves, the so-called complementarity property. They do not have a definite position but can be found with a certain probability distribution which is proportional to the square of the wave amplitude [4] as shown in Schrödinger wave equation [5, 8]:

-(ĥ²/2m) d² ψ/dx² + V ψ = i ĥ dψ/dt (Eq. 3)

where

ψ : wave function

x: position

m: mass

ĥ = h/(2 π)

h: Planck constant

i: imaginary number with i² = -1

V: potential energy

t: time

We cannot determine exactly where the point particle is, but we can calculate the probability of finding such particle at a certain position with a high degree of accuracy. This probability is equal to ψ² where ψ is the wave amplitude at the selected position. It is a cardinal rule of quantum mechanics that in principle, it is not possible to measure precisely certain conjugate pairs of properties, such as position/momentum, simultaneously. Note that this limitation is not due to measurement errors or inadequate instruments, it is rather due to the nature of particles at subatomic level.

The complementarity property (particle/wave) is only significant for atomic particle [8]. For example, an electron moving at a few millimeters per second has a wavelength of about a fraction of a millimeter. This is large enough for is quantum effects to show up in experiments. The wavelength of a moving cow would be trillions of times smaller than atomic dimensions and are far too small to ever be detected. Quantum effects in this case would also be too small to be seen. Events occurring in the macroscopic world are essentially deterministic due to their associated wavelengths of exceedingly small size.

It is important to note that there are several mathematical models in which the behavior of a quantum system can be described. They include: Heisenberg's matrix mechanics, Dirac's transformation theory (quantum algebra), Schrödinger's wave mechanics, and Feynman’s sum-over-histories approach. The equations of these models have been proved to be mathematically equivalent [3, 9]. This proof strengthens the validity of quantum theory. No matter what mathematical formalism is used, modeling of quantum behavior leads to equivalent sets of equations. Schrödinger's wave mechanics is the most well known and is also the most widely taught in academic curriculum. Even though the waves described in Schrödinger's wave mechanics may suggest some physical representation of particles, they in fact are not real physical waves and are strictly complex vibrations in an imaginary mathematical space of complex numbers called configuration space [3].

4. Entanglement and non-locality

In quantum mechanics, all the parts in an experiment set are interconnected with each other and the probabilities for all possible outcomes are open. The act of observing the system would force collapsing the wave functions and only one outcome would become the real event. In particle interferometers, a single particle such as a photon or an electron is found to travel along two paths (through two slits) at once and, once brought back together on a detection screen, giving rise to an interference pattern. The interference pattern provides proof that the particle must have traveled through both slits at once. The particle wave function is in a superposition of two components traveling along both paths instantaneously. If one attempts to detect what path the particle has just traveled through, the wave functions are collapsed and the particle is found to travel through only one path, and not the other. The interference pattern is no longer seen when the particle is being observed. The entanglement of a quantum system and a macroscopic entity, such as a measuring device, would collapse the wave function in a process called decoherence (more on this in section 6).

Entanglement of particles in a quantum system also allows for supra-luminal influence between them. This faster-than-light transmission violates the speed limit in special relativity, and also indicates that non-locality is an essential aspect of reality. This non-locality property in quantum mechanics was validated at University of Paris in 1982 [6]. In this experiment, which showed violation of Bell's inequality, two photons coming from the same source correlated their polarization state with each other after being separated by a distance. Changing the polarization of one photon instantly changed that of the other photon "on-the-flight". However far apart the two entangled particles are, they remain connected quantum-mechanically through their common wave function. When measurement of certain property is made on one of them, their common wave function collapses and the other particle is instantly endowed with the corresponding property.

5. Contrast between general relativity and quantum mechanics

The collections of 5 properties - uncertainty, complementarity, probability, disturbance of measured system by the observer, and non-locality - are together key concepts in quantum mechanics.

In the Copenhagen interpretation back in 1927, Bohr stressed the sharp contrast between general relativity and quantum mechanics [3]. General relativity describes the world in terms of space-time coordinates and absolute causality whereas quantum mechanics incorporates the interference by the observer with the system being observed. Coordinates in space-time represent position and causality depends on precise momentum of measured objects. Generality assumes that we know both the coordinates and momentum precisely at once. Quantum mechanics dictates that the precision of space-time coordinates has to be paid for in terms of uncertainty in momentum, and vice versa. All one can do is to calculate the probability that a particular event will come up with a particular result. Nevertheless, the calculated results based on quantum theory have been validated with very high degree of accuracy. For example, the process of radioactive decay is subject to the probability rules of quantum mechanics [8]. While one can never predict when an individual nucleus decays by emitting an alpha particle, one can calculate the half-life of a statistically large sample of nuclei. The half-life is the time it takes for half of the nuclei in the sample to decay.

It is impressive that quantum mechanics predicts very precisely the properties of atoms and their constituent particles, as well as the nature of the forces that hold them together (the electromagnetic, strong, and weak forces). This stellar record of predictive power, which has survived numerous challenges, is the sign of a successful scientific theory. While the formalism of quantum mechanics is not in doubt, we have not yet found a satisfactory explanation, or interpretation, of quantum phenomena in a logical manner as experienced in the everyday world. Human observers are familiar with causal events with large objects that can be visualized. Classic theories can be used to establish correlation between these causal events. It appears that when human observers attempt to measure events at subatomic scale, paradoxes seem to appear since particles do not follow classic mechanics. General relativity is a classic theory, in this sense, and can not be considered a fundamental description of the universe. If and when one finds a conflict between the two theories, it is quantum theory that one must turn to for the best description of the universe.

6. Interaction between general relativity and quantum mechanics

The delicate superposition of different potential states in quantum domain, upon being entangled with the macroscopic domain, cannot be maintained indefinitely. Instead, this superposition constantly disappear, decoheres [8]. Decoherence takes place whenever a quantum system is no longer isolated from its surrounding macroscopic environment. The loss of isolation can be due to any interaction between the quantum system and processes in the macroscopic domain including the act of measurement (using an instrument to measure the position of an electron, for example). While a macroscopic measurement device (described by the laws of classical mechanics) is ultimately composed of subatomic particles, it must not be treated as being equally subject to quantum rules. In fact, decoherence is one of the fastest and most efficient physical processes in physics. Through decoherence, quantum entities change their probabilistic properties into deterministic properties that we are all familiar with in the macroscopic world.

Subatomic particles change their properties from probabilistic (quantum) to deterministic (relative relativity) through decoherence. This decoherence is due to entanglement of the quantum particles with processes in the surrounding macroscopic world. These macroscopic processes can be measurements of a quantum system but they do not have to be limited to just measurements. By giving the observer a privileged status of collapsing the wave function of quantum particles, the Copenhagen interpretation denies the existence of an objective reality that exists in the absence of observation. In this article, it is proposed that collapsing of wave function, through decoherence, is not strictly limited to the act of measurement by any conscious observer.

The concept of entanglement has a profound effect on all objects in the universe. Virtually everything in the observable universe consists of particles that have been interacting with each other right back through time to the Big Bang when all the energy was in close proximity [3]. This indicates entanglement of all the particles in the universe at anytime in its history. The outcome from this entanglement (quantum mechanical or probabilistic in nature) is expected to eventually affect outcome beyond the subatomic domain and carry on all the way to macroscopic and cosmic scale. Beyond the subatomic domain, the outcome follows a deterministic manner through general relativity. It is also important to note that outcomes on macroscopic scale in turn affect subatomic particles by changing properties such as potential energy and coordinates of these same particles. This change in properties will eventually put constraints on their wave functions. In light of this mutual effect, quantum mechanics and general relativity are in fact dynamically interacting with each other through their subatomic domain and macroscopic domain, respectively (see Fig. 1).

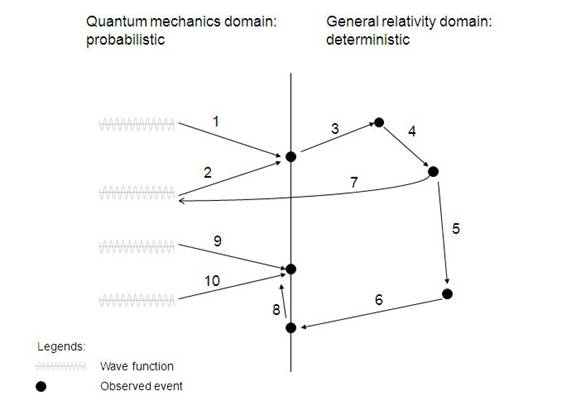
Fig 1. Interaction between general relativity and quantum mechanics:

Description of processes

1, 2: collapsing of wave functions due to macroscopic process 7 to yield an observable event (decoherence)

3, 4, 5, 6: deterministic processes with one event leading to another

7: an event in general relativity domain affects wave function properties of particles in quantum domain

8: observing a quantum system with a macroscopic device

9, 10 observing a quantum system with macroscopic process 8 causes collapsing of wave functions (decoherence)

7. The Schrödinger’s cat

A well-known paradox has been brought up by Schrödinger, one of the founders of quantum mechanics, to ponder the implications of quantum behavior in everyday life [8]. In this thought experiment, a cat (known as the Schrödinger’s cat) is shut in a box with a device containing a radioactive nucleus. The particle emitted by this nucleus when it decays would trigger a detector to release a lethal dose of poisonous gas into the box and the cat would be instantly killed. According to quantum theory, the exact moment of radioactive decay cannot be determined exactly. All one can say is that there is a certain probability that the nucleus will have decayed after a certain period of time. With quantum superposition, the wave function of the nucleus must be composed of two parts: a decayed nucleus and an undecayed nucleus. Since the fate of the cat is now dependent on the sate of decay of the radioactive nucleus, the cat’s wave function itself will also be split into two superimposed states: one describing a dead cat and the other a living cat! Until we open the box to check on the cat and see how exactly it is at that instant, we cannot say that the cat is dead or alive. This ridiculous conclusion is precisely the point of the Schrödinger’s cat paradox. However, if one considers the process of decoherence in this thought experiment, the paradox may be resolved [8]. The reason for the cat not suspended in both states of dead and alive is that decoherence takes place inside the box regardless of when we open it. The radioactive nucleus (a quantum entity) is entangled with the radioactive detector (a macroscopic device) and gives rise to decoherence with a definitive outcome in the fate of the cat in the macroscopic world.

Conclusion

Quantum theory is the fundamental description of nature at subatomic level which is probabilistic. As one approaches larger space-time scale of the macroscopic world, general relativity becomes dominate and events appear deterministic between large-scale objects. Events occurring in the macroscopic world are essentially deterministic due to their associated wavelengths of exceedingly small size. In the subatomic world, where particles and wave aspects of reality are equally significant, objects do not behave in any way that one can understand from experience of the everyday world. There is simply no physical analogy that one can create to understand the process inside atoms. Attempts to combine the two theories into a unified theory may be a futile attempt in theoretical physics. Instead, the two may be seen as two complementary theories that model processes in subatomic domain and cosmic scale. Through decoherence, quantum entities change their probabilistic properties into deterministic properties in the macroscopic world. In this article, it is proposed that decoherence is not limited to the act of measurement by any conscious observer. Subatomic processes affect cosmic processes, and vice versa, providing a dynamic interaction between the two domains. Quantum mechanics and general relativity are at work together in all natural phenomena and should not be seen as isolated theories applicable to isolated domains.

References

1. Isham, C. Chapter 5: Quantum Gravity, In: The New Physics. Ed: Davies, P. (Cambridge University Press, Cambridge, 1989).

2. Stenger, V. The Comprehensible Cosmos (Prometheus Books, 2006. p 22, 294).

3. Gribbins, J. In Search of the Schrödinger's Cat (Bantam Book, 1984. p16, 119, 114, 175, 229)

4. Georgi, H. Chapter 16: Effective Quantum Field Theories. In: The New Physics. Ed: Davies, P. (Cambridge University Press, 1989).

5. Penrose, R. The Road to Reality (Vintage Books, 2004. p 498, 958).

6. Physical Review Letters (Vol 49, p1804).

7. Smolin, L. The Trouble with Physics (First Mariner Books, 2007, p5, p238-258).

8. Al-Khalidi, J. Quantum: a Guide for the Perplexed. (Weidenfeld & Nicolson, 2003. p49, 61, 63, 89, 115, 125).

9. Herbert, N. Quantum Reality (Anchor Books, 1987, p43).